Question

Determine whether the three points are the vertices of a right triangle (6,4),(12,6),(16,-6). What geometric property is being determined in this statement?

A) Collinearity
B) Parallelism
C) Right triangle
D) Isosceles triangle

Answer 1

The three points (6,4), (12,6), and (16,-6) do not form the vertices of a right triangle.

Thus option d is correct.

Step-by-step explanation:

In order to determine if these points form a right triangle, we need to examine the slopes of the lines formed by connecting these points. For a right triangle, the slopes of two perpendicular sides should satisfy the condition: the product of their slopes should be -1.

Calculating the slopes of the line segments formed by these points:

1. Slope between (6,4) and (12,6):

Slope
`\(m_1 = \frac{{6 - 4}}{{12 - 6}} = (2)/(6) = (1)/(3)\)`

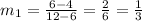
2. Slope between (6,4) and (16,-6):

Slope
`\(m_2 = \frac{{-6 - 4}}{{16 - 6}} = (-10)/(10) = -1\)`

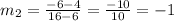
3. Slope between (12,6) and (16,-6):

Slope
`\(m_3 = \frac{{-6 - 6}}{{16 - 12}} = (-12)/(4) = -3\)`

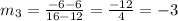
The product of
`\(m_1\)` and
`\(m_2\)` is
`\(m_1 * m_2 = (1)/(3) * (-1) = -(1)/(3)\)`, which is not equal to -1. Hence, the lines formed by connecting these points do not have perpendicular slopes, indicating that these points do not form the vertices of a right triangle.

Therefore, the geometric property being determined in this statement is the presence of a right triangle, and in this case, the points (6,4), (12,6), and (16,-6) do not satisfy the conditions to form a right triangle based on the slopes of the lines formed by connecting them.

Therefore option d is correct.