Question

Can you make this an ordered pair
y=1/2x+6
y=-x-3

Answer 1

The intersection point is (-6, 3) where the lines y = 1/2x + 6 and y = -x - 3 intersect.

Certainly! To find the point where these two equations intersect, solve them simultaneously.

Given equations:

`\(y = (1)/(2)x + 6\)`

`\(y = -x - 3\)`

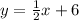
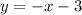
Since both equations represent lines, the point of intersection occurs where \(y\) and \(y\) are equal, so we can set the two equations equal to each other:

`\((1)/(2)x + 6 = -x - 3\)`

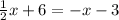
Now, solve for \(x\):

`\((1)/(2)x + x = -3 - 6\)`

`\(1.5x = -9\)`

`\(x = (-9)/(1.5) = -6\)`

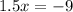
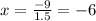
Once you have \(x = -6\), substitute it into either equation to find \(y\). Let's use the second equation for this example:

`\(y = -(-6) - 3\)`

`\(y = 6 - 3 = 3\)`

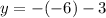
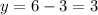
Thus, the point of intersection is
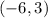`\((-6, 3)\)`, which is the ordered pair where both equations intersect in the coordinate plane.