Question

The population of bacteria in a Petri dish doubles every 24 hours the population of the bacteria is initially 500 organisms how long will it take for the population of the bacteria to reach 800 round your answer to the nearest tenth of an hour

Answer 1

Based on an exponential growth function, the time it will take for the population of the bacteria to reach 800 is 16.3 hours.

To solve this problem, we can use the formula for exponential growth:

N =
`N_0 * 2^((t/24))`

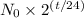
Where:

The final population = N

The initial population =
`N_0`

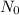
The time in hours = t

The initial population of bacteria in the Petri dish = 500 organisms

Doubling time = every 24 hours

The final required population, N = 800 organisms

Equation:

`[800 = 500 * 2^((t/24))]`

Solving for (t), we get:
`[2^((t/24)) (800)/(500) ]`

=
`1.6 [(t)/(24)]`

=
`\log_2(1.6) \approx 0.6786] \\t \approx 24 * 0.6786`

= 16.2864

approx 16.3

Thus, we can conclude that it will take approximately 16.3 hours for the population of bacteria to reach 800.