1 Answer

David Van Rijn · Answer 1 · 2024-01-05T09:16:48+0000

a. Surface area of the cube
$($SA_{\text{cube}}$)$ : 96
cm^2

Surface area of the rectangular prism
$($SA_{\text{prism}}$)$ : 112
cm^2

b. the difference between the surface areas of the cube and the rectangular prism is
$16 \, \text{cm}^2$ .

Let's denote the side length of the cube as "a" and the dimensions of the rectangular prism as length (l), width (w), and height (h).

Given that the volumes are equal, we have:

$a^3 = l * w * h$

For the cube, all sides are equal, so
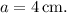
$$a = 4 \, \text{cm}$.$

For the rectangular prism, we are given that
$l = 8 \, \text{cm}\), $w = x \, \text{cm}$, and \(h = 2 \, \text{cm}$ .

Let's substitute these values into the volume equation:

$4^3 = 8 * x * 2$

Solving for
$x$ :

$64 = 16x$

$x = (64)/(16) = 4$

Now that we know
$x$ , we can find the dimensions of the rectangular prism:
$l = 8 \, \text{cm}\), $w = 4 \, \text{cm}$, \(h = 2 \, \text{cm}$ .

Now let's move on to the surface areas:

a. Surface area of the cube
$($SA_{\text{cube}}$)$ :

$SA_{\text{cube}} = 6a^2$

$SA_{\text{cube}} = 6 * (4 \, \text{cm})^2 = 6 * 16 \, \text{cm}^2 = 96 \, \text{cm}^2$

Surface area of the rectangular prism
$($SA_{\text{prism}}$)$ :

$SA_{\text{prism}} = 2lw + 2lh + 2wh$

$SA_{\text{prism}} = 2(8 * 4) + 2(8 * 2) + 2(4 * 2) = 64 + 32 + 16 = 112 \, \text{cm}^2$

b. Now, the difference between the two surface areas is:

$|\Delta SA| = |SA_{\text{prism}} - SA_{\text{cube}}|$

$|\Delta SA| = |112 - 96| = 16 \, \text{cm}^2$

So, the difference between the surface areas of the cube and the rectangular prism is
$16 \, \text{cm}^2$ .

Please log in or register to add a comment.