Question

Which rules define the function graphed below

Y=2x+3; y=-1/3x+3
Y=2x; y=-1/3x
Y=3x+2; y=3x-1
Y=-3x+3; y=x+3

Answer 1

A rule that defines the function graphed above include the following: A. y = 2x + 3; y = -1/3(x) + 3.

In Mathematics and Geometry, the slope-intercept form of the equation of a straight line refers to the general equation of a linear function and it is represented by this mathematical equation;

y = mx + b

Where:

• m represents the slope.
• x and y are the points.
• b represents the y-intercept.

First of all, we would determine the slope of the upward sloping line by using these points (0, 3) and (-1, 1);

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

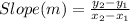
Slope (m) = (1 - 3)/(-1 - 0)

Slope (m) = -2/-1

Slope (m) = 2

At y-intercept (0, 3) and a slope of 2, an equation for this line can be calculated by using the slope-intercept form as follows:

y = mx + b

y = 2x + 3

For the slope of the downward sloping line, we have;

Slope (m) = (2 - 3)/(3 - 0)

Slope (m) = -1/3

At y-intercept (0, 3) and a slope of -1/3, an equation for this line can be calculated by using the slope-intercept form as follows:

y = mx + b

y = -1/3(x) + 3