Question

A building is constructed using bricks that can be modeled as right rectangular prisms with a dimension of 7\frac{3}{4}7 4 3 ​ in by 3\frac{1}{2}3 2 1 ​ in by 2\frac{1}{2}2 2 1 ​ in. If the bricks cost $0.10 per cubic inch, find the cost of 1250 bricks. Round your answer to the nearest cent.

Answer 1

The cost of 1250 bricks, rounded to the nearest cent, is $8476.56.

How did we get the value?

To find the cost of 1250 bricks, we first need to calculate the volume of one brick and then multiply it by the number of bricks.

The dimensions of one brick are:

- Length:
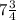`7(3)/(4)` inches

- Width:
`3(1)/(2)` inches

- Height:
`2(1)/(2)` inches

The volume of a rectangular prism is given by the formula:
`\( \text{Volume} = \text{Length} * \text{Width} * \text{Height} \).`

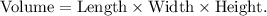
Let's calculate the volume of one brick:

`\[\text{Volume of one brick} = 7(3)/(4) * 3(1)/(2) * 2(1)/(2)\]`

To perform the calculation, it's easier to convert the mixed numbers to improper fractions:

`\[\text{Volume of one brick} = \left( (31)/(4) \right) * \left( (7)/(2) \right) * \left( (5)/(2) \right)\]`

Now, multiply the numerators and denominators:

`\[\text{Volume of one brick} = (31 * 7 * 5)/(4 * 2 * 2)\]`

`\[\text{Volume of one brick} = (1085)/(16) \text{ cubic inches}\]`

Now, multiply the volume of one brick by the number of bricks (1250) and the cost per cubic inch ($0.10):

`\[\text{Total cost} = 1250 * (1085)/(16) * 0.10\]`

`\[\text{Total cost} = (1250 * 1085 * 0.10)/(16)\]`

Calculate the total cost and round it to the nearest cent.

Total cost =
`(135625)/(16)`

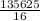
Total cost = 8476.5625

Total cost
`\approx 8476.56`

So, the cost of 1250 bricks, rounded to the nearest cent, is $8476.56.