Question

Suppose that the function g is defined, for all real numbers, as follows.

gx{3 if x #0
{1 if x=0
Graph the function g.

Answer 1

The graph of function
`\(g\)` displays a horizontal line at
`\(y = 3\)` and a hole at
`\(x = 0\)`. For all real numbers except 0,
`\(g(x)\)` is constant at 3, with
`\(g(0) = 1\).`

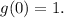
The function
`\(g\)` is represented graphically by a horizontal line situated at
`\(y = 3\)`. However, a hole appears at
`\(x = 0\)`. This peculiarity arises from the fact that for all real numbers excluding 0,
`\(g(x)\)` holds a constant value of 3, while
`\(g(0)\)` equals 1.

Executing the graphing process involves drawing a straight line parallel to the x-axis at
`\(y = 3\)`. Simultaneously, a distinctive point is marked at the origin (0, 1) to denote the hole in the graph. This visual representation accurately captures the behavior of
`\(g(x)\)` as a constant function except at
`\(x = 0\)`, where the anomaly is reflected in the presence of a hole.

In summary, the graph effectively illustrates the consistent value of 3 for
`\(g(x)\)` except at
`\(x = 0\)`, where
`\(g(0)\)` deviates, causing a hole in the graph.