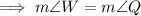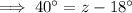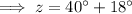Question

Help me please. Your the best if you help.

Answer 1

`x= \boxed{25}\;\; \sf meters`

`y= \boxed{15}\;\; \sf meters`

`z= \boxed{58}\;\; \sf degrees`

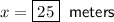
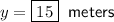
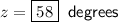
Explanation:

Similar Triangles

• Corresponding sides are always in the same ratio.
• Corresponding angles are the same size.

If ΔWXY ~ ΔQRS then:

• WX : QR = XY : RS = WY : QS

Therefore:

`\implies \sf WX : QR = XY : RS = WY : QS`

`\implies (15+x) : 30 = 20 : y = 32 : 24`

`\implies (15+x)/(30)=(20)/(y)=(32)/(24)`

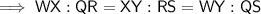
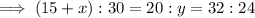
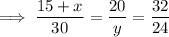
Solving for x:

`\implies (15+x)/(30)=(32)/(24)`

`\implies 15+x=(30 \cdot 32)/(24)`

`\implies x=(30 \cdot 32)/(24)-15`

`\implies x=25`

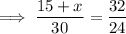
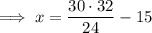
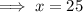
Solving for y:

`\implies (20)/(y)=(32)/(24)`

`\implies 20 \cdot 24=32y`

`\implies y=(20 \cdot 24)/(32)`

`\implies y=15`

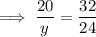
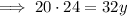
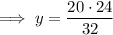
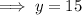
If ΔWXY ~ ΔQRS then:

• m∠W = m∠Q
• m∠X = m∠R
• m∠Y = m∠S

Therefore, solving for z:

`\implies m \angle W = m \angle Q`

`\implies 40^(\circ) = z-18^(\circ)`

`\implies z=40^(\circ) +18^(\circ)`

`\implies z=58^(\circ)`