Question

When the polynomial P(x) = 3x3 – 2x2 + kx – 12 is divided by x – 3, the remainder is 0. Which of the following is also a factor of P(x)?

A. 3x-4
B. x+1
C. x-4
D. 3x+1

Answer 1

Step-by-step explanation: bro st op

Answer 2

B. x + 1

Explanation:

If the polynomial P(x) = 3x³ - 2x² + kx - 12 is divided by (x - 3) and the remainder is zero, then according the Factor Theorem, this means that f(3) = 0.

Therefore, to find the value of k, we can substitute x = 3 into P(x), set it to zero, and solve for k:

`\begin{aligned}P(3)&=0\\3(3)^3-2(3)^2+k(3)-12&=0\\3(27)-2(9)+3k-12&=0\\81-18+3k-12&=0\\3k+51&=0\\3k&=-51\\k&=-17\end{aligned}`

Therefore, as the value of k is -17, the polynomial P(x) in standard form is:

`P(x) = 3x^3- 2x^2 -17x - 12`

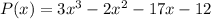
To factor P(x), begin by dividing the polynomial by (x - 3) using long division:

`\large \begin{array}{r}3x^2+7x+4\phantom{)}\\x-3{\overline{\smash{\big)}\,3x^3-2x^2-17x-12\phantom{)}}\\{-~\phantom{(}\underline{(3x^3-9x^2)\phantom{-bbbbbbbb))}}\\7x^2-17x-12\phantom{)}\\-~\phantom{()}\underline{(7x^2-21x)\phantom{bbbb)}}\\4x-12\phantom{)}\\-~\phantom{()}\underline{(4x-12)}\\0\phantom{)}\end{array}`

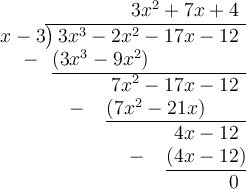
Therefore:

`P(x)=(x-3)(3x^2+7x+4)`

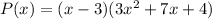
Finally, factor the quadratic factor:

`\begin{aligned}3x^2+7x+4&=3x^2+3x+4x+4\\&=3x(x+1)+4(x+1)\\&=(3x+4)(x+1)\end{aligned}`

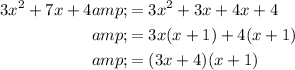
Therefore, the fully factored polynomial P(x) is:

`P(x)=(x-3)(3x+4)(x+1)`

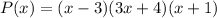
So, the factors of polynomial P(x) are:

• 
  `(x-3)`
• 
  `(3x+4)`
• 
  `(x+1)`