Question

5(2t+4)
area model ? ​

Answer 1

The expression
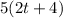`\(5(2t+4)\)` can be represented using an area model to help visualize the concept. The expression represents the area of a rectangle, where the length is given by
`\(5\)` and the width is given by
`\(2t+4\)`.

```

+------------------+

| |

| |

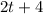| | 5

| |

| |

+------------------+

2t+4

```

The expression
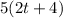`\(5(2t+4)\)` can be represented using an area model to help visualize the concept. The expression represents the area of a rectangle, where the length is given by
`\(5\)` and the width is given by
`\(2t+4\)`.

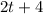Let's break it down:

- The length of the rectangle is
`\(5\)`.

- The width of the rectangle is
`\(2t+4\)`.

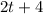The area
`(\(A\))` of a rectangle is given by the formula
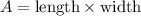`\(A = \text{length} * \text{width}\)`. In this case:

`\[A = 5 * (2t+4)\]`

To create an area model, you can draw a rectangle and label its length and width. The length of the rectangle is \(5\), and the width is \(2t+4\). Then, you can express the area as the product of the length and width.

```

+------------------+

| |

| |

| | 5

| |

| |

+------------------+

2t+4

```

So, the area model represents the expression
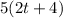`\(5(2t+4)\)` as the area of the rectangle formed by the length
`\(5\)` and the width
`\(2t+4\)`.

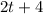The probable question may be

"How can you use an area model to represent the expression
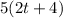`\(5(2t+4)\)`?"