Question

PLEASE HELP** in each following problems, draw a right triangle for each problem, then substitute values and solve. the first one has already been solved

Answer 1

2. Suitcase Diagonal: For a
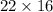`\(22 * 16\)` inch suitcase, the diagonal is approximately 27.39 inches.

3. Right Triangle Leg: In a right triangle with hypotenuse 25 and leg 7, the other leg is 24.

4. Jogging Distance: After running 6 miles north and 9 miles west, the shortest distance back is approximately 10.82 miles.

5. Ladder Height: A 104 ft ladder reaches 96 ft up a wall 40 ft away.

6. Pond Crossing Savings: Walking 10 m south and 24 m east saves approximately 25 m.

7. Rectangle Length: In a rectangle with width 15 inches and diagonal 17 inches, the length is 8 inches.

8. Tent Tallest Point: A tent with slanted sides of 11 ft each and a 12 ft base has a peak height of approximately 12.53 ft.

9. Pole Shadow Distance: A 12 ft pole casts a 16 ft shadow, with 12 ft between the shadow end and the top.

10. Biking Shortest Distance: After biking 33 km south and 56 km west, the shortest distance to the starting point is approximately 64.24 km.

Let's solve each problem one by one:

2. Suitcase Diagonal Length:

- Given a rectangle (the suitcase) with length 22 inches and height 16 inches.

- Using the Pythagorean Theorem:
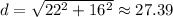`\(d = √(22^2 + 16^2) \approx 27.39\)` inches.

3. Right Triangle Leg Length:

- Given a right triangle with hypotenuse 25 and one leg 7.

- Using the Pythagorean Theorem:
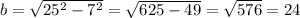`\(b = √(25^2 - 7^2) = √(625 - 49) = √(576) = 24\)` units.

4. Shortest Distance Jogging:

- Two legs of the jog form a right triangle with sides 6 miles and 9 miles.

- Using the Pythagorean Theorem:
`\(d = √(6^2 + 9^2) = √(36 + 81) = √(117) \approx 10.82\)` miles.

5. Ladder Height on Wall:

- Given a ladder with length 104 feet and base 40 feet from the wall.

- Using the Pythagorean Theorem:
`\(h = √(104^2 - 40^2) = √(10816 - 1600) = √(9216) = 96\)` feet.

6. Savings by Walking Through the Pond:

- Given a right-angled triangle with legs 10 meters and 24 meters.

- Using the Pythagorean Theorem:
`\(s = √(10^2 + 24^2) \approx 25\)` meters.

7. Rectangle Length:

- Given a rectangle with width 15 inches and diagonal 17 inches.

- Using the Pythagorean Theorem:
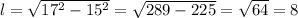`\(l = √(17^2 - 15^2) = √(289 - 225) = √(64) = 8\)` inches.

8. Tallest Point of the Tent:

- Given a tent with slanted sides of length 11 feet and the bottom 12 feet across.

- Using the Pythagorean Theorem:
`\(h = \sqrt{11^2 + \left((12)/(2)\right)^2} = √(121 + 36) = √(157) \approx 12.53\)` feet.

9. Pole Shadow Distance:

- Given a pole with a shadow length of \(16\) feet and a pole length of 12 feet.

- Using similar triangles:
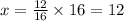`\(x = (12)/(16) * 16 = 12\)` feet.

10. Shortest Distance Biking:

- Two legs of the biking form a right triangle with sides 33 km and 56 km.

- Using the Pythagorean Theorem:
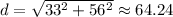`\(d = √(33^2 + 56^2) \approx 64.24\)` km.

Note: In each solution, the Pythagorean Theorem is used (
`\(c^2 = a^2 + b^2\)`) to find the missing side or length.