Question

URGENT!!!!

Use the information to answer the question.
The perimeter of the floor in Emilio's rectangular bedroom is 52 feet. The width of the floor is 12 feet.
What is the area of Emilio's bedroom floor? Enter the answer in the box.
Square feet

Answer 1

168feet^2

Explanation:

52-24=28

28/2=14

14x12=168

Answer 2

Area =
`\boxed{\sf \;\; 168 \;\;}` Square Feet

Explanation:

The perimeter of a rectangle is given by the formula:

`\sf \textsf{Perimeter} = 2(\textsf{Length} + \textsf{Width})`

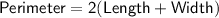
In this case, we're given that the width is 12 feet and the perimeter is 52 feet.

Substitute these values into the formula and solve for the length:

`\sf 52 = 2(\textsf{Length} + 12)`

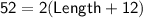
Divide both sides by 2:

`\sf (52)/(2) =\frac{\cancel{ 2}(\textsf{Length} + 12) }{\cancel{2}}`

`\sf 26 = \textsf{Length} + 12`

Subtract 12 from both sides:

`\sf 26 -12= \textsf{Length} + 12-12`

`\sf 14 = \textsf{Length}`

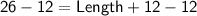
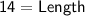
Now that we know the length (
`\sf 14` feet) and the width (
`\sf 12` feet) of the rectangle, we can find the area (
`\sf A`) using the formula:

`\sf \textsf{Area} = \textsf{Length} * \textsf{Width}`

`\sf \textsf{Area} = 14 * 12`

`\sf \textsf{Area} = 168`

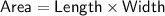
Therefore, the area of Emilio's bedroom floor is
`\sf 168` square feet.