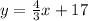Answer:
Explanation:
The table shows a set of x and y values, thus showing a set of points we can use to find the equation.
1) First, find the slope by using two points and substituting their x and y values into the slope formula,
 . I chose (-3, 13) and (0,17), but any two points from the table will work. Use them for the formula like so:
. I chose (-3, 13) and (0,17), but any two points from the table will work. Use them for the formula like so:
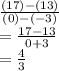
Thus, the slope is
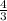 .
.
2) Next, identify the y-intercept. The y-intercept is where the line hits the y-axis. All points on the y-axis have a x value of 0. Thus, (0,17) must be the y-intercept of the line.
3) Finally, write an equation in slope-intercept form, or
 format. Substitute the
format. Substitute the
 and
and
 for real values.
for real values.
The
 represents the slope of the equation, so substitute it for
represents the slope of the equation, so substitute it for
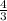 . The
. The
 represents the y-value of the y-intercept, so substitute it for 17. This will give the following answer and equation:
represents the y-value of the y-intercept, so substitute it for 17. This will give the following answer and equation: