Question

A particle of mass m has half the kinetic energy of another particle of mass m/2. The ratio of the speeds of the lighter and heavier particles is

A. 1:1
B. 1:2
C. 2:1
D. 1:4

Answer 1

The ratio of the speeds of the lighter particle to heavier particles is 2 : 1 (option C)

How to calculate the ratio of the speeds of the particles?

First, we shall write the kinetic energy for the various particles. Details below:

For heavier particle:

• Mass (m) = m
• Velocity (v) = v
• Kinetic energy of heavier particle (KE) =?

`KE = (1)/(2)mv^2`

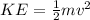
For lighter particle:

• Mass (m) =
  `m_l` =
  `(1)/(2) m`
• Velocity (v) =
  `v_l`
• Kinetic energy of lighter particle (
  `KE_l`) =?

`KE_l = (1)/(2)m_lv_l^2\\\\KE_l = (1)/(2)\ *\ (m)/(2)\ *\ v_l^2\\\\KE_l = (1)/(4)mv_l^2`

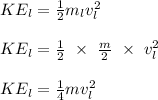
We were told that:

KE of heavier particle = half of KE of lighter particle

Thus, we:

`(1)/(2)mv^2 = (1)/(2)\ *\ (1)/(4)mv_l^2\\\\(1)/(2)mv^2 = (1)/(8)mv_l^2\\\\v^2 = (1)/(4)v_l^2\\\\4v^2 = v_l^2\\\\(v_l^2)/(v^2) = 4\\\\(v_l)/(v) = √(4) \\\\(v_l)/(v) = 2\\\\v_l\ :\ v = 2\ :\ 1`

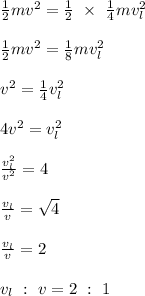
Thus, the ratio is 2 : 1. The correct answer is option C