Question

Find the slant height of the largest possible cone that can be inserted in a hemisphere of volume 144πcm³

(a) 9√2 cm
(b) 12√2 cm
(c) 6√2 cm
(d) 7 √2 cm​

Answer 1

The slant height of the largest possible cone that can be inserted in a hemisphere is c. 6
`√(2)`

The volume of the hemisphere is given by:

Volume of hemisphere =
`(2)/(3) \pi r^(3)`

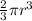
Given the volume as 144π
`cm^(3)`

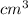
So, to set the equation,

144π = 2/3 * π *
`r^(3)`

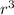
144π * 3 = 2 * π *
`r^(3)`

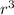
432π = 2π
`r^(3)`

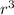
divide through by 2π

432π/2π = 2π
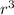`r^(3)`/2π

216 =
`r^(3)`

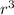
r = ∛216

r = 6

So, radius of the hemisphere = 6 cm

The slant height (l) of the cone can be found using the Pythagorean theorem in the right triangle formed by the radius (r), the height (h) of the cone.

So, l² = h² + r²

Where the height of the cone is the radius of the hemisphere,

l² = 2r²

l =
`\sqrt{2r^(2) }`

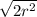
l =
`√(2)` * r

l =
`√(2)` * 6

l = 6
`√(2)`

Therefore, the slant height of the largest possible cone that can be inserted in a hemisphere is c. 6
`√(2)`