Question

In a Young's double-slit experiment, the separation between the slits is 0.15 mm. In the experiment, a source of light of wavelength:

(a) λ = 600 nm, will produce a diffraction pattern.

(b) λ = 450 nm, will produce a more spread-out interference pattern.

(c) λ = 750 nm, will produce a narrower interference pattern.

(d) λ = 350 nm, will produce no interference pattern.

Answer 1

In the experiment, a source of light of wavelength:

• (c) λ = 750 nm, will produce a narrower interference pattern.
• (d) λ = 350 nm, will produce no interference pattern.

How to find source of light?

In a Young's double-slit experiment, the condition for constructive interference (bright fringes) is given by the formula:

`\[ d \sin \theta = m \lambda \]`

where:

d = separation between the slits,

θ = angle of the bright fringe,

m = order of the fringe (an integer),

λ = wavelength of light.

If m = 1, the condition for the first-order bright fringe ( m = 1) is:

`\[ d \sin \theta = \lambda \]`

Now, analyze the given situations:

(a) λ = 600 nm:

`\[ d \sin \theta = 0.15 \, \text{mm} * \sin \theta = 600 \, \text{nm} \]`

`\[ \sin \theta = \frac{600 \, \text{nm}}{0.15 \, \text{mm}} = 4 \]`

Since
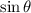`\( \sin \theta \)` cannot be greater than 1, this situation will not produce a diffraction pattern.

(b) λ = 450 nm:

`\[ d \sin \theta = 0.15 \, \text{mm} * \sin \theta = 450 \, \text{nm} \]`

`\[ \sin \theta = \frac{450 \, \text{nm}}{0.15 \, \text{mm}} = 3 \]`

This situation will not produce a well-defined diffraction pattern.

(c) λ = 750 nm nm:

`\[ d \sin \theta = 0.15 \, \text{mm} * \sin \theta = 750 \, \text{nm} \]`

`\[ \sin \theta = \frac{750 \, \text{nm}}{0.15 \, \text{mm}} = 5 \]`

This situation will produce a narrower interference pattern.

(d) λ = 350 nm:

`\[ d \sin \theta = 0.15 \, \text{mm} * \sin \theta = 350 \, \text{nm} \]`

`\[ \sin \theta = \frac{350 \, \text{nm}}{0.15 \, \text{mm}} = 2.333 \]`

This situation will not produce a clear interference pattern.

So, the correct statements are:

(c) λ = 750 nm will produce a narrower interference pattern.

(d) λ = 350 nm will produce no interference pattern.