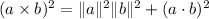The correct option is:
a)
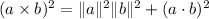
Let's use the vector triple product identity to show that
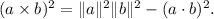
The vector triple product identity is given by:
![\[ (a * b)^2 = \|a\|^2 \|b\|^2 - (a \cdot b)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/iquf8ys1bbkny5ax6vy37wgz6x9vbz5r6s.png)
Now, let's prove this identity step by step:
1. **Expand the left side:**
![\[ (a * b)^2 = (a * b) \cdot (a * b) \]](https://img.qammunity.org/2024/formulas/physics/high-school/m8mbkaah0f9u2tsuw6v9qe6eimdtuvlrpy.png)
2. **Apply the vector triple product:**
![\[ (a * b)^2 = (a \cdot (b * a))^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/7ebiyhqohaf8lmpy30552t5cgse2gsu69y.png)
3. **Apply the scalar triple product:**
![\[ (a * b)^2 = ((a \cdot b) \cdot a - (a \cdot a) \cdot b)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/30yr49oyxynu5ky5z6nrv95gbbqe8v7w2g.png)
4. **Distribute and simplify:**
![\[ (a * b)^2 = ((a \cdot b) a - \|a\|^2 b)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/sh02lwnrea8otwpvskajsunmv00ys3af3n.png)
5. **Expand and simplify further:**
![\[ (a * b)^2 = (a \cdot b)^2 \|a\|^2 - 2 (a \cdot b) \|a\|^2 \|b\|^2 + \|a\|^4 \|b\|^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/y9mo80u4cl0oq37bupfk6qteurxb7w71s3.png)
6. **Combine terms:**
![\[ (a * b)^2 = (a \cdot b)^2 \|a\|^2 - (a \cdot b) \|a\|^2 \|b\|^2 + \|a\|^4 \|b\|^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/xduzbmab2novjxqbsn2ex23cpk1zl26xej.png)
7. **Combine like terms and factor out a common factor:**
![\[ (a * b)^2 = \|a\|^2 \|b\|^2 - (a \cdot b)^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/iquf8ys1bbkny5ax6vy37wgz6x9vbz5r6s.png)
Now, we have shown that
 , which matches the given expression.
, which matches the given expression.
Conclusion:
The correct option is:
a)