The three fractions are:
![\[ A = (35)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b47gtmnkhcxs8bity37fzk07nseggfx8bi.png)
![\[ B = (5)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/90pwcgn55v3jykqzobztkeui3386o8iv3m.png)
![\[ C = (66)/(13) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b4q1wp1vgnavkvjvhksbghzlenau8hxe3h.png)
Let's denote the three fractions as A, B, and C, with A being the greatest, B being the middle, and C being the smallest fraction.
Given that the sum of the three fractions is
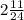 , we can set up the equation:
, we can set up the equation:
![\[A + B + C = 2 (11)/(24)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fgayd5xzihujib72x1w71xv2n1a81xy6fo.png)
Now, we are told that if the greatest fraction (A) is divided by the smallest fraction (C), the result is
 , and this result is greater than the middle fraction (B) by
, and this result is greater than the middle fraction (B) by
 . This can be expressed as two equations:
. This can be expressed as two equations:
![\[ (A)/(C) = (7)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/34wam2qvgkrjijftvcmiezjkmxteq5ushw.png)
![\[ (A)/(C) - B = (1)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wealdmxr30bya9kuxgd787ygszvonzju2k.png)
Now, let's solve these equations simultaneously.
Equation 1:
![\[ A + B + C = 2 (11)/(24) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/swwk7gxmrmd6n6nk7jtozdqv0tctclrjll.png)
Equation 2:
![\[ (A)/(C) = (7)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/34wam2qvgkrjijftvcmiezjkmxteq5ushw.png)
Equation 3:
![\[ (A)/(C) - B = (1)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wealdmxr30bya9kuxgd787ygszvonzju2k.png)
First, let's deal with Equation 2:
![\[ (A)/(C) = (7)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/34wam2qvgkrjijftvcmiezjkmxteq5ushw.png)
Cross-multiply to get:
![\[ 6A = 7C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uwewrjbhl0ixm0ys179k5hzmgo629i99fx.png)
Now, substitute this into Equation 1:
![\[ 6A + 6B + 6C = 2 \cdot 35 + 11 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ywdioit8chwxa54gw9caudbclmmm0gx3bg.png)
Simplify:
![\[ 6A + 6B + 6C = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xc7j0g3tl1t24z3kh39vpvgjjtvy3aa3uf.png)
Now, substitute
 into the equation:
into the equation:
![\[ 7C + 6B + 6C = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yn0eixnqkzin9d0xyod8l38ixqg5p1znwm.png)
Combine like terms:
![\[ 13C + 6B = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o2bltht2afy5m2gs6g2gdiwsgazrg6dzu9.png)
Now, consider Equation 3:
![\[ (A)/(C) - B = (1)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wealdmxr30bya9kuxgd787ygszvonzju2k.png)
Substitute
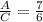 into this equation:
into this equation:
![\[ (7)/(6) - B = (1)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7l29mr1tka9ea32r47bkpzlj3hz5e9o0k5.png)
Multiply through by 6 to get rid of the fraction:
![\[ 7 - 6B = 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/i3fgw8gl9s9tm13z8dxrolxt3rqr6p6ak4.png)
Now, solve for B:
![\[ -6B = -5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/q8myj8ys90qcsd4cwvzj9mkatpukida89f.png)
![\[ B = (5)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/90pwcgn55v3jykqzobztkeui3386o8iv3m.png)
Now that we have B, substitute it back into the equation we derived earlier:
![\[ 13C + 6B = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o2bltht2afy5m2gs6g2gdiwsgazrg6dzu9.png)
![\[ 13C + 6 \cdot (5)/(6) = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y3cgsj8iue5bto15cczlzp015xbddtt3t9.png)
![\[ 13C + 5 = 71 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dhzxglwydijnphyrgrkbjiavnfx3ruojep.png)
![\[ 13C = 66 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kphbnxzzmayywew6qwqn6rszue9o9mdg8c.png)
![\[ C = (66)/(13) = 5 (1)/(13) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cdiq9aoqsxoi5eeb70reilqa7qeqj5jn48.png)
Now that we have B and C, we can find A using the relationship
 :
:
![\[ 6A = 7 \cdot (66)/(13) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y4tjc2r1ew66r5qwpootnv0b6njj23f4ha.png)
![\[ 6A = 7 \cdot 5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wsc7u25fga8ue1ctuqdpjj2cyr2uiukl3o.png)
![\[ 6A = 35 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dsao3enpm4ggyc8sybn9xjmvi19wy7ovrk.png)
![\[ A = (35)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b47gtmnkhcxs8bity37fzk07nseggfx8bi.png)
So, the three fractions are:
![\[ A = (35)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b47gtmnkhcxs8bity37fzk07nseggfx8bi.png)
![\[ B = (5)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/90pwcgn55v3jykqzobztkeui3386o8iv3m.png)
![\[ C = (66)/(13) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b4q1wp1vgnavkvjvhksbghzlenau8hxe3h.png)