Question

Liam is going to drive from his house to City A without stopping. Let D represent Liam's distance from City At hours after

leaving his house. A graph of D is shown below. Write an equation for D then state the y-intercept of the graph and
determine its interpretation in the context of the problem.
Distance Remaining to City A (Miles)
Number of Hours Driving

Answer 1

The equation representing Liam’s remaining distance to City A over time is
`D=-60t+360`

. The y-intercept is 360 miles; this indicates that initially Liam was positioned 360 miles away from City A before embarking on his journey. This equation and interpretation provide a mathematical model of Liam’s journey, reflecting the constant rate at which he is approaching City A

The graph provided in the problem represents Liam's journey from his house to City A. The Y-axis of the graph represents the distance remaining to City A (D), and the X-axis represents the number of hours driving. The graph is a straight line with a negative slope, indicating that as time progresses, Liam's distance to City A decreases at a constant rate.

From the graph, we can see that Liam starts at 360 miles away from City A and after 6 hours of driving, he arrives in City A (D=0). This gives us two points on the graph: (0,360) and (6,0). We can use these points to find the slope (m) of the line using the formula
`$$m = (y2 - y1)/(x2 - x1)$$, giving us $$m = (0 - 360)/(6 - 0) = -60$$.`

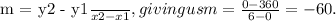
With this slope, we can use point-slope form or slope-intercept form to write an equation for D. Using point-slope form with one of our points and rearranging gives us
`$$D = -60t + 360$$`.

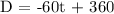The y-intercept of this function is 360 which represents Liam's initial distance from City A before he begins his journey. In other words, at t=0 hours after leaving his house, Liam is 360 miles away from City A. This interpretation aligns with real-world logic; before commencing his drive towards City A without stopping along the way, Liam would be at his starting distance from it.