The value of
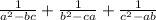 is
is
 .
.
How did we get the value?
To find the value of
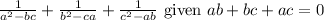 , let's try to express each denominator in terms of the given condition.
, let's try to express each denominator in terms of the given condition.
Given
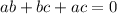 , we can rewrite each term in the denominators as follows:
, we can rewrite each term in the denominators as follows:
1.
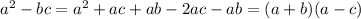
2.
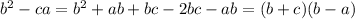
3.
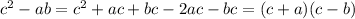
Now, substitute these expressions back into the given expression:
![\[(1)/((a + b)(a - c)) + (1)/((b + c)(b - a)) + (1)/((c + a)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kxbado2vclx1lmw45n7qowb806whnmez2s.png)
Next, factor out the common denominators:
![\[((b + c) + (a - c))/((a + b)(a - c)) + ((c + a) + (b - a))/((b + c)(b - a)) + ((a + b) + (c - b))/((c + a)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hfoxlc6qrrim42hmqssb77n7liknpnttg6.png)
Combine the numerators:
![\[(2a)/((a + b)(a - c)) + (2b)/((b + c)(b - a)) + (2c)/((c + a)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uwe0gong76opa4iv7by088ugfwll7zpn8s.png)
Now, substitute the expressions we found for the denominators:
![\[(2a)/((a + b)(a - c)) + (2b)/((b + c)(b - a)) + (2c)/((c + a)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uwe0gong76opa4iv7by088ugfwll7zpn8s.png)
Now, use the given condition
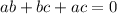 to simplify the expression:
to simplify the expression:
![\[(2a)/((a + b)(a - c)) + (2b)/((b + c)(b - a)) + (2c)/((c + a)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uwe0gong76opa4iv7by088ugfwll7zpn8s.png)
![\[= (2a)/((-c)(a - c)) + (2b)/((-a)(b - a)) + (2c)/((-b)(c - b))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ufx7x9xao150ehwpjzcq8zz4hwrs5u17xu.png)
![\[= (2)/(c) + (2)/(a) + (2)/(b)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aot5ijrt1kvycy7rlm5ov9shti1fp6mazx.png)
Combine the fractions:
![\[= (2(a + b + c))/(abc)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r143eprv62qbmjlrli0h28ma3gbiomb0j0.png)
Since
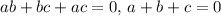 , so the expression simplifies to:
, so the expression simplifies to:
![\[= (2 \cdot 0)/(abc) \\ = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lc1spj0vnzn7o7vtsrh6w4icqtgfj8rkg2.png)
Therefore, the value of
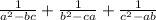 is
is
 .
.