If in still water he can swim with a speed 5/3 times that of the current, then the speed of the current, in m/min is (A.) 30.
How to find speed?
Denote the speed of the man in still water as
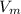 and the speed of the current as
and the speed of the current as
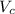 .
.
The effective speed is the width of the river divided by the time taken:
![\[ \text{Effective speed} = \frac{\text{Width of the river}}{\text{Time taken}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/207daf4xkfu18wxkjq5xbf4cux04yze4bo.png)
Given that width is 320 m and the time taken is 4 min:
![\[ V_m + V_c = \frac{320 \, \text{m}}{4 \, \text{min}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/tzljovwajj8hxgy0xdgzavkqea9uf0zn75.png)
Since the man swims with a speed
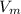 that is 5/3 times that of the current:
that is 5/3 times that of the current:
![\[ V_m = (5)/(3) V_c \]](https://img.qammunity.org/2024/formulas/physics/high-school/vt9rhyd2rgkdx2z2d0e2iuyqzufi2xe9oc.png)
Now, substitute this relationship into the effective speed equation:
![\[ (5)/(3) V_c + V_c = \frac{320 \, \text{m}}{4 \, \text{min}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/qnobmeamzpfm3t9j6hw0gmgn3bw4y7g79r.png)
Combine the terms on the left side:
![\[ (8)/(3) V_c = 80 \, \text{m/min} \]](https://img.qammunity.org/2024/formulas/physics/high-school/c9fb0ci72alnnzz4ixpmagqi6pjdzw2r25.png)
Now, solve for
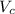 :
:
![\[ V_c = (3)/(8) * 80 \, \text{m/min} \]](https://img.qammunity.org/2024/formulas/physics/high-school/cqrquycy3r4xk1r3b3gk5jtxj16xgyax04.png)
![\[ V_c = 30 \, \text{m/min} \]](https://img.qammunity.org/2024/formulas/physics/high-school/s7hzdb356pk3q1lvg1bvo4f0dcc7hd8glf.png)
So, the speed of the current is 30 m/min, and the correct answer is A. 30.