Question

A rectangle has a length of 22 feet less than 8 times its width. If the area of the rectangle is 580 square feet, find the length of the rectangle.​

Answer 1

• 58feet

Explanation :

let the length of the rectangle be l and the width be w .

ATQ,

• l = 8w - 22

we know that,

• area of a rectangle = length x width

since the area of the rectangle is given to us as 580ft^2 ,we can find the length of the rectangle by plugging in the value of length as 8w - 22,

• (8w - 22) x w = 580
• 8w^2 - 22w = 580
• 8w^2 - 22w -580 = 0

now, we can factorise the expression using the double split method

• 8w^2 - 22w -580
• 2(4w^2 -11w - 290)
• 2(4w^2 +29w -40w - 290)
• 2(w(4w + 29) -10(4w + 29))
• 2((4w + 29)(w-10))

thus,

• w = 10 or -29/4

since the width can't be negative thus,

• width = 10ft

hence,

the measure of the length would be

• length = 8w -22ft
• length = 8*10ft - 22ft
• length = 80ft - 22ft
• length = 58ft

therefore,the length of the rectangle would be equal to 58ft.

Answer 2

length of the rectangle = 58 feet

Explanation:

Let's denote the width of the rectangle as
`\sf w` and the length as
`\sf l`. We are given two pieces of information:

• The length of the rectangle is 22 feet less than 8 times its width:
  `\sf l = 8w - 22`.
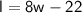• The area of the rectangle is 580 square feet:
  `\sf \text{Area} = l * w = 580`.

Now, we can set up an equation using these two pieces of information:

`\sf l * w = 580`

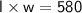
Substitute the expression for
`\sf l` from the first piece of information:

`\sf (8w - 22) * w = 580`

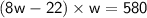
Now, distribute and rearrange to form a quadratic equation:

`\sf 8w^2 - 22w - 580 = 0`

To solve this quadratic equation, we can use the quadratic formula:

`\sf w = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}`

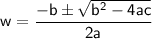
In this case,
`\sf a = 8`,
`\sf b = -22`, and
`\sf c = -580`.

Substitute these values into the formula:

`\sf w = \frac{{22 \pm \sqrt{{(-22)^2 - 4(8)(-580)}}}}{{2(8)}}`

`\sf w = \frac{{22 \pm \sqrt{{484 + 18560}}}}{{16}}`

`\sf w = \frac{{22 \pm \sqrt{{19044}}}}{{16}}`

`\sf w = \frac{{22 \pm 138}}{{16}}`

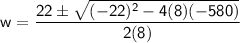
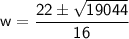
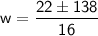
Now, consider both solutions:

• When
  `\sf w = \frac{{22 + 138}}{{16}} = \frac{{160}}{{16}} = 10`
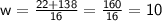
• When
  `\sf w = \frac{{22 - 138}}{{16}} = \frac{{-116}}{{16}} = -7.25` (discard because width cannot be negative)

So, the width of the rectangle is
`\sf 10` feet. Now, use the first piece of information to find the length:

`\sf l = 8w - 22`

`\sf l = 8(10) - 22`

`\sf l = 80 - 22`

`\sf l = 58`

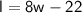
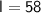
Therefore, the length of the rectangle is
`\sf 58` feet.