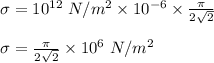Question

Standing wave produced in a metal rod of length 1 m fixed at the left end is represented by the equation y=10⁻⁶sin πx/2 ​sin200pt where x is in metre and t is in seconds. The maximum tensile stress at the midpoint of the rod is : (Young's modulus of material of rod=10¹² N/m² )

(1) 2π​×10⁶ N/m²
(2) 2π×10⁶ N/m²
(3) 22​π​×106 N/m²

Answer 1

The maximum tensile stress is determined as
`(\pi)/(2√(2) ) * 10^6 \ N/m^2`.

How to calculate the maximum tensile stress?

The maximum tensile stress is calculated by applying the following formula as shown below.

Young's modulus (Y) = Tensile stress (σ) / Tensile strain (ε)

σ = Yε

σ = Y (dy/dx)

The given parameters include;

Young's modulus = 10¹² N/m²²

wave equation, y = 10⁻⁶ sin πx/2 · sin 200πt

The tensile stain of the rod is;

dy/dx = 10⁻⁶ × π/2 cos πx/2 · sin 200πt

At maximum tensile stress;

sin 200πt = 1

x = L/2

x = 1 m / 2 = 0.5

dy/dx = 10⁻⁶ × π/2 cos π(0.5)/2 · (1)

dy/dx = 10⁻⁶ × π/2 cos π/₄ · (1)

dy/dx = 10⁻⁶ × π/2 cos (45)

dy/dx = 10⁻⁶ × π/2 × 1/√2

`(dy)/(dx) = 10^(-6) * (\pi )/(2 √(2) )`

The tensile stress becomes;

σ = Y (dy/dx)

`\sigma = 10^(12) \ N/m^2 * 10^(-6) * (\pi)/(2√(2) ) \\\\\sigma = (\pi)/(2√(2) ) * 10^6 \ N/m^2`