Question

mohan invested some amount in scheme a for 3 years at x% per annum compounded annually. he invested the same amount in scheme b for 3 years, at 24% rate of interest, compounded semi annually. the interest received is the same in both the schemes. what is the value of x?

Answer 1

The value of x is 12.

This means Mohan invested in Scheme A at a rate of 12% per annum compounded annually to achieve the same interest received as in Scheme B with a 24% per annum interest rate compounded semiannually.

How to find the value of x:

To find the value of x, set up an equation based on the given information.

Let's assume the principal amount invested by Mohan in both Scheme A and Scheme B is P.

For Scheme A:

The interest is compounded annually, so the formula for calculating the amount after 3 years with a principal of P and an interest rate of x% per annum compounded annually is:

`A = P(1 + x/100)^3`

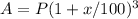
For Scheme B:

The interest is compounded semiannually, so the formula for calculating the amount after 3 years with a principal of P and an interest rate of 24% per annum compounded semiannually is:

`A = P(1 + r/2)^6`

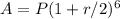
Since the interest received is the same in both schemes, we can set up the equation:

`P(1 + x/100)^3 = P(1 + 24/200)^6`

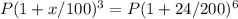
Simplifying the equation:

`(1 + x/100)^3 = (1 + 12/100)^6`

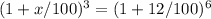
Taking the cube root of both sides:

1 + x/100 = 1 + 12/100

x/100 = 12/100

x = 12

Therefore, the value of x is 12.

This means Mohan invested in Scheme A at a rate of 12% per annum compounded annually to achieve the same interest received as in Scheme B with a 24% per annum interest rate compounded semiannually.