Question

Two triangles are shown in the graph. Proving that the two shapes are congruent requires that a set of transformations maps the original shape onto the new shape. Which set of transformations proves that the shapes are congruent

Answer 1

The set of transformation that proves that the shapes are congruent are a rotation 90° about the origin and a reflection about the y-axis which can be represented as follows;

`r_(y-axis)\circ R_(O,\, 90^(\circ))(x,\, y)`

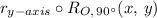
The steps used to find the set of transformation that proves that the shapes are congruent are presented as follows;

The coordinates of the vertices of the original shape and the new shape indicates that the transformation from the original shape to the new shape is; (x, y) → (-y, -x)

The transformation (x, y) → (-y, -x) corresponds to a rotation of 90° clockwise about the origin(x, y) → (y, -x), followed by a reflection about the y-axis (y, -x) → (-y, -x)

The coordinates of the image are therefore;

Transformation; Rotation 90° Clockwise about the Origin

(2, 5) → Rotation 90° Clockwise about the Origin → (5, -2)

(2, 3) → Rotation 90° Clockwise about the Origin → (3, -2)

(7, 3) → Rotation 90° Clockwise about the Origin → (3, -7)

Transformation; Reflection about the y-axis

(5, -2) → Transformation → (-5, -2)

(3, -2) → Transformation → (-3, -2)

(3, -7) → Transformation → (-3, -7)

The coordinates of the above image corresponds with the coordinated os the vertices of the image of the original triangle

The vertices of the possible triangles obtained from a similar question found through search are;

Original shape (2, 5), (2, 3), (7, 3)

New shape (-5, -2), (-3, -2), (-3, -7)