Question

On a coordinate plane, Dan graphed two triangles, △PQR and △TSR, with coordinates of the vertices as follows: P(1,6), Q(7, 4), R(3,2), S(−3,−1), and T(6,−4). Dan wants to prove △PQR∼△TSR. Cheryl suggests that he show PQ ∥ TS. In the blanks below,

(1) use the calculator to enter the slopes of PQ and TS
(2) complete the congruence statement
Slope of PQ = ___
Slope of TS = ___
∠P≅∠ ___

Answer 1

Dan aims to prove △PQR ∼ △TSR with vertices P(1,6), Q(7,4), R(3,2), S(−3,−1), and T(6,−4). Calculating slopes, Cheryl suggests PQ ∥ TS, but the attempt is incorrect. Dan should explore other pairs of corresponding sides and angles for an accurate similarity proof.

To prove the similarity between triangles △PQR and △TSR, Dan can demonstrate that the corresponding sides are proportional and the corresponding angles are congruent. Cheryl suggests focusing on the parallelism of sides PQ and TS.

(1) To find the slopes, use the formula: slope =
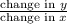`\(\frac{\text{change in } y}{\text{change in } x}\)`. For PQ:

`\[ \text{Slope of PQ} = (4 - 6)/(7 - 1) = -(2)/(6) = -(1)/(3) \]`

For TS:

`\[ \text{Slope of TS} = ((-1) - (-4))/((-3) - 6) = (3)/(9) = (1)/(3) \]`

(2) The congruence statement:

`\[ \text{Slope of PQ} = -(1)/(3) \]`

`\[ \text{Slope of TS} = (1)/(3) \]`

`\[ \angle P \cong \angle T \]`

The slopes of PQ and TS are negative reciprocals, indicating that the lines are perpendicular, not parallel. To prove the similarity, Dan should focus on other pairs of corresponding sides and angles, as the current attempt to show parallelism is not accurate.