Question

An oil company is interested in estimating the true proportion of female truck drivers based in five southern states. A statistician hired by the oil company must determine the sample size needed in order to make the estimate accurate to within 3% of the true proportion with 90% confidence. What is the minimum number of truck drivers that the statistician should sample in these southern states in order to achieve the desired accuracy?

a) 771
b) 752
c) 733
d) 742
e) 759
f) None of the above

Answer 1

The minimum sample size needed is 752.

Therefore, the correct answer is option b) 752.

How to determine the minimum sample size

To determine the minimum sample size needed to estimate the true proportion with a desired level of accuracy and confidence, use the formula for sample size calculation in estimating a proportion:

`n = (Z^2 * p * (1-p)) / E^2`

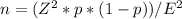
Where:

n = sample size

Z = Z-score corresponding to the desired confidence level

p = estimated proportion (0.5 is a conservative estimate when the true proportion is unknown)

E = desired margin of error (in this case, 3% or 0.03)

Since the question states a 90% confidence level, the corresponding Z-score is approximately 1.645.

Plug in the values:

`n = (1.645^2 * 0.5 * (1-0.5)) / 0.03^2`

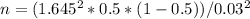
n ≈ (2.705025 * 0.25) / 0.0009

n ≈ 0.67625625 / 0.0009

n ≈ 751.395

Rounding up to the nearest whole number, the minimum sample size needed is 752.

Therefore, the correct answer is option b) 752.