Question

PLSSS HELP ME ITS FOR A PROJECT PLS GIVE INFORMATION ON HOW TO DO IT

Answer 1

In triangle ABC with additional lines PQ and MN, corresponding angles
`\(\angle PBA \cong \angle QBC\)` and
`\(\angle BAM \cong \angle BCN\)`. Supplementary angles
`\(\angle PBA + \angle BAM = 180^\circ\)`, proving the triangle angle sum theorem.

To prove that the sum of the interior angles of a triangle is equal to 180 degrees, we can consider the triangle ABC and the additional lines PQ and MN. Let's denote the angles as follows:

-
`\(\angle PBA = d\)`

-
`\(\angle BAM = f\)`

-
`\(\angle QBC = e\)`

-
`\(\angle BCN = g\)`

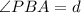
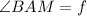
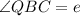
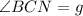
Now, let's analyze the pairs of angles to see which ones must be congruent and which ones are supplementary:

1. Congruent Angles:

-
`\(\angle PBA\) and \(\angle QBC\)` must be congruent. This is because they are corresponding angles between parallel lines PQ and MN, cut by transversal line BC.

-
`\(\angle BAM\) and \(\angle BCN\)` must be congruent. Similar to the first case, these are corresponding angles between parallel lines PQ and MN, cut by transversal line BA.

So, we can say:

`\(\angle PBA \cong \angle QBC\) and \(\angle BAM \cong \angle BCN\).`

2. Supplementary Angles:

- The pair
`\(\angle PBA\) and \(\angle BAM\)` must be supplementary. This is because they form a linear pair within the triangle ABC.

So, we can say:

`\(\angle PBA + \angle BAM = 180^\circ\).`

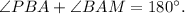
Now, let's use these relationships to prove that the sum of the interior angles of triangle ABC is equal to 180 degrees:

`\[ \angle PBA + \angle BAM + \angle QBC = \angle PBA + \angle BAM + \angle PBA \cong \angle PBA + \angle BAM + \angle BAM = 180^\circ. \]`

Therefore, the sum of the interior angles of triangle ABC is equal to 180 degrees, and we used the congruent and supplementary relationships between the angles to establish this result.