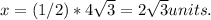To find the value of x in the triangle ABC with a 30° angle at C, we recognize that it's a 30°-60°-90° triangle and use the formula relating the sides. Resulting in
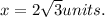
Step-by-step explanation:
The triangle ABC with AB = x units, BC = y units, and CA = 4\sqrt{3} units, and given \angleBCA = 30°, we can use the Law of Sines or trigonometric ratios in a right-triangle to find the value of x. However, the direct method here would be to apply trigonometry since we are dealing with a 30° angle, which implies that triangle ABC is a right-angled triangle.
Using the formula for the lengths in a 30°-60°-90° triangle, where the side opposite the 30° angle (x) is half the length of the hypotenuse (CA). Therefore, x = (1/2) * CA, substituting the length of CA yields