To find the value of
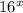 given the equation
given the equation
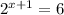 , we can use the fact that 16 can be expressed as
, we can use the fact that 16 can be expressed as
 . By substituting this into the expression we want to evaluate, we get:
. By substituting this into the expression we want to evaluate, we get:

Now, let's substitute this expression into the given equation:
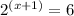
Replace
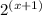 with
with

To find the value of x, we can take the logarithm of both sides. Let's use the natural logarithm (ln):
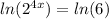
Using the logarithmic property
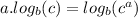 , we can bring down the exponent:
, we can bring down the exponent:
4x⋅ln(2)=ln(6).
Now, solve for

Now that we have the value of x, substitute it back into the expression
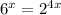 :
:
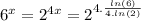
Simplify the expression:
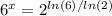
Now, use the property
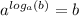
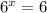
Therefore, the value of is
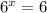 .
.