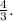Question

Line I has the equation 4x-3y=15 line m is shown below. what is the slope of the steeper line

Answer 1

The slope of line m, passing through consecutive points (-6, 0) and (-4, 1), is
`\((1)/(2)\)`. Comparing with the slope of line l,
`\((4)/(3)\)`, the steeper line is l.

To determine the slope of line m, you can select two points on the line and use the slope formula
`\(\text{Slope} = \frac{\text{Change in } y}{\text{Change in } x}\)`. Let's choose two consecutive points on line m, say (-6, 0) and (-4, 1).

`\[\text{Slope of line } m = (1 - 0)/(-4 - (-6)) = (1)/(2)\]`

Now, compare this slope with the slope of line l, given by the equation 4x - 3y = 15. Rewrite it in slope-intercept form (y = mx + b) to identify the slope.

`\[4x - 3y = 15 \implies 3y = 4x - 15 \implies y = (4)/(3)x - 5\]`

The slope of line l is
`\((4)/(3)\).`

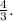
Comparing the slopes, the steeper line is the one with the greater absolute value of the slope. Therefore, the steeper line has a slope of
`\((4)/(3)\)`, and the correct answer is (A)
`\((4)/(3)\).`