Question

people immigrate into a territory at a poisson rate of λ=1 per day. what is the probability that the elapsed time between the tenth and the eleventh arrival exceeds two days?

Answer 1

The probability that the elapsed time between the tenth and eleventh arrival exceeds two days is approximately 13.53%.

In a Poisson process with a rate of λ arrivals per day, the time between arrivals follows an exponential distribution with parameter λ. Therefore, the probability of waiting more than t days for the next arrival is given by
`e^(^-^λ^t^).`

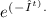
In your specific case:

We want the probability of exceeding 2 days (t = 2) between the 10th and 11th arrival.

λ = 1 arrival per day.

Therefore, the probability P of exceeding 2 days is:

`P = e^(^-^λ^t) = e^(^-^1 ^* ^2^)`

P = 0.1353

So, the probability that the elapsed time between the tenth and eleventh arrival exceeds two days is approximately 13.53%.