Question

Using calculus, it can be shown that if a ball is thrown upward with an initial velocity of 64 ft/s from the top of a building 220 ft high, then its height h above the ground t seconds later will be

h = 220 + 64t − 16t2.
During what time interval (in seconds) will the ball be at least 28 ft above the ground? (Enter your answer using interval notation.)

Answer 1

[0, 6]

Explanation:

To find at what time interval the ball will be at least 28 ft above the ground, set h equal to 28, solve for t, then find the difference between the two t-values.

Set the expression for height (h) equal to 28:

`\begin{aligned}h&=28\\\\220 + 64t-16t^2&=28\end{aligned}`

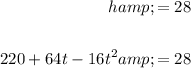
Subtract 28 from both sides of the equation and rearrange:

`\begin{aligned}192 + 64t-16t^2&=0\\\\16t^2-64t-192&=0\\\\16(t^2-4t-12&=0\\\\t^2-4t-12&=0\end{aligned}`

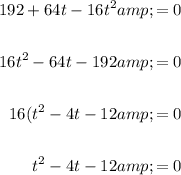
Factor the quadratic:

`\begin{aligned}t^2-6t+2t-12&=0\\\\t(t-6)+2(t-6)&=0\\\\(t+2)(t-6)&=0\end{aligned}`

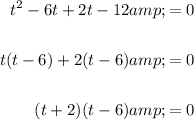
Solve for t:

`t+2=0 \implies t=-2`

`t-6=0 \implies t=6`

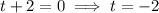
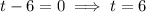
As time cannot be negative, and the ball is thrown from an initial height of 220 ft, the time interval during which the ball will be at least 28 ft above the ground is the first 6 seconds of its journey. In interval notation, this is represented as [0, 6].