Question

The 1.45-kg ball is suspended from a 0.80-m string and swung in a horizontal circle at a constant speed such that the string makes an angle of 14∘ with the vertical.

a. What is the tension in the string?

b. What is the speed of the ball?

Answer 1

a) Tension = 14.66 N

b) Speed = 0.69 m/s

Step-by-step explanation:

Part a: Tension in the String:

1. Forces on the ball:

There are two main forces acting on the ball:

• Gravity (mg): Downward force due to its weight (mg = 1.45 kg × 9.81 m/s²)
• Tension (T): Upward force exerted by the string

2. Resolving forces:

Since the ball is moving in a horizontal circle, the net force acting on it must be directed towards the center of the circle (centripetal force). We can resolve the forces into horizontal and vertical components:

• Horizontal: Tension balances the horizontal component of gravity (T cos θ)
• Vertical: Tension balances the vertical component of gravity (T sin θ)

3. Solving for tension:

From the vertical component:

`\sf T \sin \theta = mg`

`\sf T = (mg)/(\sin \theta)`

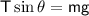
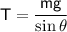
The weight of the swinging ball is balanced by the component(T cos θ), so

`\sf T \cos \theta = mg`

`\sf T = (mg)/(\cos \theta)`

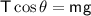
Substituting the given values:

`\sf (m = 1.45 \, \textsf{kg}, g = 9.81 \, \textsf{m/s}^2, \theta = 14^\circ)`

`\sf T = \frac{(1.45 \, \textsf{kg} * 9.81 \, }{\cos(14^\circ)}`

`\sf T \approx 14.65996357 \, \textsf{N}`

`\sf T \approx =14.66 \, \textsf{N (in 2 d.p.)}`

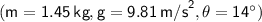
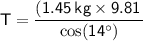
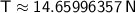
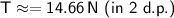
Therefore, the tension in the string is approximately 14.66 N.

Part b: Speed of the Ball:

1. Centripetal force:

The centripetal force acting on the ball can be calculated using the formula:

`\sf F_c = (mv^2)/(r)`

where:

• m is the mass of the ball (1.45 kg)
• v is the speed of the ball (unknown)
• r is the radius of the circle (0.80 m)

2. Equating forces:

From the horizontal component, the tension provides the centripetal force:

The component
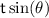`\sf t \sin(\theta)` provides the necessary centripetal force, therefore

`\sf T \sin \theta = F_c`

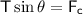
Substituting the expression for
`\sf F_c`:

`\sf T \sin \theta = (mv^2)/(r)`

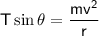
3. Solving for speed:

Rearranging for v:

`\sf v^2 = (Tr \sin \theta)/(m)`

`\sf v^2 = (T \cdot L\sin(\theta)\cdot \sin \theta)/(m)`

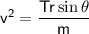
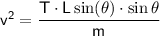
Substituting the values for T, θ, and m:

`\sf v^2 = \frac{(14.66 \, \textsf{N}) \cdot 0.80m \cdot \sin(14^\circ) \cdot \sin(14^\circ) \, }{1.45 \textsf{kg}}`

`\sf v^2 \approx 0.4733760796 \, \textsf{m}^2/\textsf{s}^2`

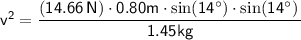
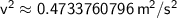
Taking the square root (note that only the positive root makes sense in this context):

`\sf v \approx \sqrt{0.4733760796 \, \textsf{m}^2 \textsf{s}^2}`

`\sf v \approx 0.6880233133 \, \textsf{m/s}`

`\sf v \approx 0.69 \textsf{m/s (in 2 d.p.)}`

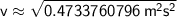
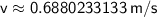
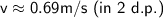
Therefore, the speed of the ball is approximately 0.69 m/s.