The triangles shown are similar can set up the proportion as follows to find x.
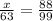
To create a proportion to find
 using the similar triangles, you would set up a ratio comparing the corresponding sides of the triangles. The sides that correspond to each other are proportional.
using the similar triangles, you would set up a ratio comparing the corresponding sides of the triangles. The sides that correspond to each other are proportional.
Two triangles are considered similar if their corresponding angles are equal, and their corresponding sides are in proportion. In other words, if you can match up the angles of one triangle with the angles of another triangle, and the ratios of the lengths of their corresponding sides are equal, then the triangles are similar
Given the two triangles, you can set up the proportion as follows:
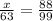
Now you can solve for
 by cross-multiplying and then dividing by the coefficient of
by cross-multiplying and then dividing by the coefficient of
 .
.
The value of
 is 56.
is 56.
Therefore The triangles shown are similar can set up the proportion as follows to find x.
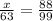
The probable two triangles for the given question is