Question

Why does dividing by a fraction give a bigger number?

Answer 1

Understanding why dividing by a fraction results in a larger number involves grasping two key mathematical principles: the concept of fractions and the nature of division.

1. Concept of Fractions:

• A fraction represents a part of a whole. When you have a fraction like
  `(1)/(2)`, it means one part of something that is divided into two equal parts.
• Smaller the denominator, larger the individual parts. For instance,
  `(1)/(2)` is larger than
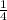  `(1)/(4)`, even though they both represent a single part, because in
  `(1)/(2)`, the whole is divided into fewer parts.

2. Nature of Division:

• Division is essentially the operation of finding out how many times a number (divisor) can fit into another number (dividend).
• When you divide by a whole number greater than 1, you're finding out how many of those larger pieces fit into your number, which naturally leads to a smaller result. For example, 10 ÷ 2 asks how many times 2 fits into 10, which is 5 times.

Now, combining these two concepts when dividing by a fraction:

• Dividing by a fraction like
  `(1)/(2)` is asking the question, "How many
  `(1)/(2)`'s fit into my number?" Since
  `(1)/(2)` is smaller than 1, you can fit more
  `(1)/(2)`'s into any number than you could fit 1's.
• The smaller the fraction you divide by, the more of those fractions will fit into the number, leading to a larger result. For instance, if you divide 10 by
  `(1)/(2)`, you're essentially asking how many halves fit into 10, which would be 20 halves.

Application:

This principle is applied in various real-world situations. For example, if you have a recipe that requires
`(1)/(2)` cup of an ingredient and you only have a
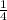`(1)/(4)` cup measure, you would need to use it twice (since
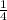`(1)/(4)` is smaller than
`(1)/(2)`), thus illustrating how dividing by a smaller fraction (in this case, using a smaller measure) results in a larger number (more uses of the measure).

Answer 2

Because you're multiplying by reciprocal

Explanation:

Because you're multiplying by reciprocal:

example:

1/2 / 1/4 = 1/2 * 4

1/2 / 1/4 = 4/2

4/2 = 2