The approximate value of the given integral is:
![(1)/(2) [(e^4 + e^(-4))-2]](https://img.qammunity.org/2024/formulas/mathematics/college/sozmxpl2wjflzbjm5adykxdewwyhlerzvg.png)
To evaluate the integral
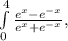
we can use the u-substitution method. Let
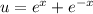 . then,
. then,
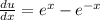
and solving for dx, we get
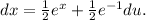
Now, we can substitute u and dx into the integral:
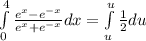
To determine the new limits of integration, we substitute x=0 and x=4 into the expression for u:
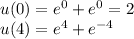
Now, we can rewrite the integral in terms of u:
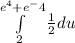
Integrating with respect to u, we get:
![\int\limits^(e^4+e^-4)_2 (1)/(2) du= (1)/(2) [u]^{e^4+e^(-4)}_2](https://img.qammunity.org/2024/formulas/mathematics/college/6rfx68khzlksmn5bdyy2geqturat95sywu.png)
Substituting the limits:
![(1)/(2) [(e^4 + e^(-4))-2]](https://img.qammunity.org/2024/formulas/mathematics/college/sozmxpl2wjflzbjm5adykxdewwyhlerzvg.png)
So, the approximate value of the given integral is:
![(1)/(2) [(e^4 + e^(-4))-2]](https://img.qammunity.org/2024/formulas/mathematics/college/sozmxpl2wjflzbjm5adykxdewwyhlerzvg.png)