Question

How is a hyperbola formed? Explain the transverse axis and conjugate axis of a hyperbola and what they can tell us about a hyperbola.

Answer 1

The transverse and conjugate axes provide information about the orientation, size, and shape of the hyperbola. They help visualize the hyperbola and locate its important elements, such as vertices and foci, which are essential for understanding its geometric properties.

What is a hyperbola?

A hyperbola is a type of conic section, formed by the intersection of a plane with a double cone. It has two distinct branches, each resembling a curve that opens in opposite directions. The standard form of the equation for a hyperbola centered at the origin is given by:

`\[(x^2)/(a^2) - (y^2)/(b^2) = 1\]`

or

`\[(y^2)/(b^2) - (x^2)/(a^2) = 1\]`

The parameters
`\(a\)` and
`\(b\)` determine the shape and orientation of the hyperbola. The center of the hyperbola is at the origin
`\((0,0)\).`

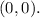
The transverse axis and conjugate axis are important elements in understanding the characteristics of a hyperbola:

1. Transverse Axis: The transverse axis is the line segment passing through the foci of the hyperbola. The length of the transverse axis is
`\(2a\)`, where
`\(a\)` is the distance from the center to either vertex along the major axis. The transverse axis also determines the direction in which the branches of the hyperbola open.

2. Conjugate Axis: The conjugate axis is perpendicular to the transverse axis and passes through the center of the hyperbola. The length of the conjugate axis is
`\(2b\)`, where
`\(b\)` is the distance from the center to a point on either branch along the minor axis.

The relationship between
`\(a\)` and
`\(b\)` determines the type of hyperbola:

- If
`\(a > b\)`, the hyperbola is horizontally oriented, and the transverse axis is along the x-axis.

- If
`\(b > a\)`, the hyperbola is vertically oriented, and the transverse axis is along the y-axis.

The distance between the center and each focus
`(\(c\))` can be found using the relationship
`\(c = √(a^2 + b^2)\)`. The foci play a crucial role in understanding the geometry and properties of the hyperbola.

In summary, the transverse and conjugate axes provide information about the orientation, size, and shape of the hyperbola. They help visualize the hyperbola and locate its important elements, such as vertices and foci, which are essential for understanding its geometric properties.