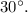In triangle ABC with angle B denoted as x, angle C as 75 degrees, and AB equal to AC, solving for x yields
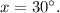
In a triangle ABC where angle B is denoted as x and angle C is 75 degrees, and AB is equal to AC, we can use the fact that the sum of interior angles in a triangle is 180 degrees.
![\[ \text{Angle A} + \text{Angle B} + \text{Angle C} = 180^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/college/3lzie1afc8q7syu9i5tu4x2p4m2d1db37w.png)
Substitute the given values:
![\[ \text{Angle A} + x + 75^\circ = 180^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2ii3wwo8a3tvf0o0e4r4kukjt8pfgzpvwc.png)
To find angle A, subtract
 from 180:
from 180:
![\[ \text{Angle A} = 180^\circ - (x + 75^\circ) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kwi4yoz8strcxfhdvo2lxx9xcls5bjeveq.png)
Since AB is equal to AC, angle A must be equal to angle C:
![\[ \text{Angle A} = 75^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/isdfzqzoj72ew1pfeszg0llp5e4m7gp200.png)
Now set up the equation:
![\[ 75^\circ = 180^\circ - (x + 75^\circ) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3lk4ccupktkfd2zdd64d6sfy85qqenvnjo.png)
Solve for x:
![\[ x = 30^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y3n46v3jtnw81z29gcoq31dfnv7l0jq2zq.png)
So, in the triangle ABC, angle B is