Question

(x3 - 3x2 - 10x + 24) by (x - 2).

Answer 1

Quotient:
`\(x^2 - 5x - 8\)`, Remainder: 8, dividing
`\(x^3 - 3x^2 - 10x + 24\)` by
`\(x - 2\)` using long division.

To divide the polynomial
`\(x^3 - 3x^2 - 10x + 24\) by \(x - 2\)`, we can use polynomial long division.

The process involves dividing term by term, starting with the highest degree term of the dividend (the polynomial being divided) by the divisor (the linear term).

Here are the steps:

`________________x - 2 | x^3 - 3x^2 - 10x + 24`

Divide
`\(x^3\) by \(x\)`, which gives
`\(x^2\)`. Multiply
`\(x - 2\) by \(x^2\) to get \(x^3 - 2x^2\)`, then subtract it from the original polynomial to get the remainder:

`x^2 ________________x - 2 | x^3 - 3x^2 - 10x + 24 -(x^3 - 2x^2) ____________ - x^2 - 10x + 24`

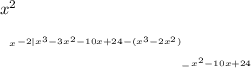
Now, bring down the next term (-10x) from the original polynomial:

`x^2 - 5x ________________x - 2 | x^3 - 3x^2 - 10x + 24 -(x^3 - 2x^2) ____________ - x^2 - 10x + 24 -(- x^2 + 2x) ____________ -8x + 24`

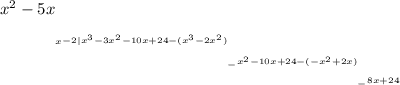
Finally, bring down the constant term (24) and divide it by \(x - 2\) to get the final remainder:

`x^2 - 5x - 8 ________________x - 2 | x^3 - 3x^2 - 10x + 24 -(x^3 - 2x^2) ____________ - x^2 - 10x + 24 -(- x^2 + 2x) ____________ -8x + 24 -(-8x + 16) __________ 8 (remainder)`

Therefore, after performing polynomial long division, the result is
`\(x^2 - 5x - 8\)` with a remainder of 8.