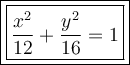Question

Write an equation for the​ ellipse, satisfying the following conditions.

Foci at ​(0,​-2) and ​(0,​2); the point ​(-3​,2​) on ellipse

Answer 1

`(x^2)/(12)+(y^2)/(16)=1`

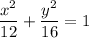
Explanation:

The foci of an ellipse lie on its major axis, which is the longest diameter of the ellipse. As the x-coordinates of the foci ​(0,​ -2) and ​(0,​ 2) are the same (x = 0), this means that the major axis is parallel to the y-axis, and the ellipse is vertical.

The general equation for a vertical ellipse is:

`\boxed{\begin{array}{l}\underline{\textsf{General equation of a vertical ellipse}}\\\\((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1\\\\\textsf{where:}\\\phantom{ww}\bullet \textsf{$2b$ is the major axis.}\\\phantom{ww}\bullet \textsf{$2a$ is the minor axis.}\\\phantom{ww}\bullet \textsf{$(h,k)$ is the center.}\\ \phantom{ww}\bullet \textsf{$(h,k\pm b)$ are the vertices.}\\ \phantom{ww}\bullet \textsf{$(h,k\pm c)$ are the foci where $c^2=b^2-a^2$}\end{array}}`

In a vertical ellipse, the x-coordinate of the center is equal to the x-coordinate of the foci, and the y-coordinate of the center is equal to the midpoint of the y-coordinates of the foci. Given that the foci are (0, -2) and (0, 2), the center of the ellipse is the origin (0, 0), so h = 0 and k = 0.

The sum of the distances from an (x, y) point on the ellipse to the foci is equal to the major axis (2a). Given that point (-3, 2) is on the ellipse, then d₁ is the distance from (-3, 2) to (0, -2), and d₂ is the distance from (-3, 2) to (0, 2). This means that d₁ + d₂ = 2b.

Use the distance formula to find the distances d₁ and d₂:

`d_1=√((0-(-3))^2+(-2-2)^2)`

`d_1=√(9+16)`

`d_1=√(25)`

`d_1=5`

`d_2=√((0-(-3))^2+(2-2)^2)`

`d_2=√(9+0)`

`d_2=√(9)`

`d_2=3`

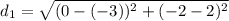
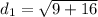
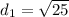
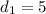
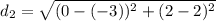
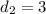
Therefore:

`\begin{aligned}d_1+d_2&=2b\\5+3&=2b\\2b&=8\\b&=4\\b^2&=16\end{aligned}`

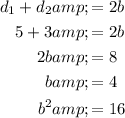
Substitute the values of h = 0 and k = 0 into the foci formula to find the value of c:

`\begin{aligned}(h, k \pm c) &=(0, \pm 2)\\(0, 0 \pm 2)&=(0, \pm 2)\\\pm c&=\pm2\\c&=2\end{aligned}`

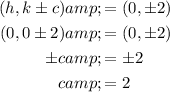
To find the value of a², substitute the values of b² and c into the formula c² = b² - a²:

`\begin{aligned}2^2&=16-a^2\\4&=16-a^2\\a^2&=16-4\\a^2&=12\end{aligned}`

Finally, substitute the values of h, k, a² and b² into the general equation of a vertical ellipse:

`((x-0)^2)/(12)+((y-0)^2)/(16)=1`

`(x^2)/(12)+(y^2)/(16)=1`

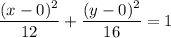
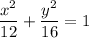
Therefore, the equation of the​ ellipse that has foci at (0, -2) and (0, 2), and passes through the point (-3, 2) is:

`\large\boxed{\boxed{(x^2)/(12)+(y^2)/(16)=1}}`