Question

I need help asap:

The lengths of a triangular plot of land
measure 19 yards, 23 yards and 27 yards.
Find the largest angle for this plot of
land.

Answer 1

79.4° to the nearest tenth of a degree

Explanation:

You are trying to find the angle opposite the side of length 27.

Let the length of that side be c and a and b be the lengths of the other two sides and let C be the measure of the angle you are looking for

Using the law of cosines

`c = \sqrt{a^(2) + b^(2) - 2abcos C}`

`27 = \sqrt{19^(2) + 23^(2) - 2(19)(23)cosC}`

`27^(2) = 19^(2) + 23^(2) - 2(19)(23)cosC`

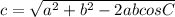
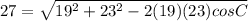
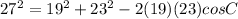
729 = 361 + 529 - 874cosC

729 = 890 - 874cosC

-161 = -874cosC

-161/-874 = cosC

.1842105.... = cosC

C = arccos .1842105.... = 79.4° to the nearest tenth of a degree