Question

Thank you, use correct sig figs

Answer 1

The electrode on the left will be positive. Using the Nernst equation with standard cell potential, concentrations, and temperature, the voltmeter will show approximately 0.02 V, assuming
`\(n = 1\).`

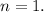
The electrode on the left will be positive in this galvanic cell configuration. The movement of electrons from the left half-cell to the right half-cell generates a potential difference, making the left electrode positive and the right electrode negative.

To determine the voltage, we can use the Nernst equation for calculating the cell potential (
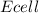`Ecell`) under non-standard conditions:

`\[Ecell = E^o - (0.0592)/(n) \cdot \log\left(([M^+]_2^n)/([M^+]_1^n)\right)\]`

Here,
`\(E^o\)` is the standard cell potential,
`\([M^+]_2\) and \([M^+]_1\)` are the molar concentrations of
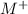`M^+` in the right and left half-cells, and \(n\) is the number of moles of electrons transferred (which is equal to the number of ions of
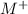`M^+` involved).

Since the right and left half-cells contain the same substance, \(n\) is likely equal to 1. The standard cell potential
`(\(E^o\))` for a galvanic cell with
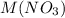`M(NO_3)` as the electrolyte can be looked up.

Given that the temperature is constant at 35.0 °C, the Nernst equation allows us to find the non-standard cell potential. Solving this equation will provide the voltage, and rounding the result to two significant digits will give the final answer.