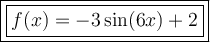Question

Write an equation for the sine function shown on the graph. Explain how you arrived at your answer. PLS HELP!

Answer 1

`f(x) = -3 \sin(6x)+2`

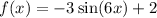
Explanation:

To write an equation for the graphed sine function, we can use the general equation of a sine function:

`f(x) = A \sin(B(x+C))+D`

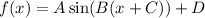
where:

• A = amplitude
• B = 2π/T (where T is the period)
• C = phase shift
• D = vertical shift

The midline of a sine graph is the horizontal line along which the sine function oscillates. It is situated at the vertical position y = D, where D is the midpoint of the maximum and minimum y-values of the function. As the maximum value of the graphed function is y = 5 and the minimum value is y = -1, then:

`D=(5+(-1))/(2)=(4)/(2)=2`

So, the midline of the graphed function is y = 2.

The amplitude is the vertical distance between the midline and the maximum (or minimum) y-value of the graph. As the maximum value of the graphed function is y = 5 and the midline is y = 2, then:

`A=5-2=3`

The behavior of the parent sine function, y = sin(x), around the origin is such that it approaches from a minimum point, passes through the origin, and then approaches a maximum point. Since the graphed function exhibits the opposite trend, it implies a reflection across the y-axis. Therefore, we negate the amplitude, so:

`A=-3`

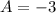
The period of a sine function is the horizontal distance between two consecutive points where the function repeats its pattern. Given that two consecutive points on the midline are (0, 2) and (π/3, 2), we can deduce that the period (T) of the graphed function is T = π/3. Therefore:

`B=(2\pi)/(T)=(2\pi)/((\pi)/(3))=6`

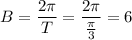
The phase shift is represented by C. It indicates how the graph is horizontally translated to the left or right. If C > 0, the graph shifts to the left, and if C < 0, the graph shifts to the right. In the parent sine function, y = sin(x), the y-intercept aligns with the midline of the function. As the y-intercept of the graphed function also aligns with the midline, it implies that the graphed function has not undergone a horizontal translation, so:

`C = 0`

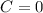
In summary:

• A = -3
• B = 6
• C = 0
• D = 2

Substituting these values into the general equation of a sine function gives:

`f(x)=-3\sin(6(x+0))+2`

So, the equation of the graphed sine function is:

`\large\boxed{\boxed{f(x) = -3 \sin(6x)+2}}`