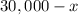Eric invested $15,000 in an account with a 9% interest rate and $15,000 in an account with a 6% interest rate. After one year, he received a total of $1,890 in interest.
Eric had $30,000 to invest last year, and he divided this sum into two accounts, aiming to maximize returns. Let's denote the amount he invested in the first account, which offered a 9% simple interest rate, as \(x\). The remaining amount,
was invested in the second account, which had a 6% simple interest rate. After one year, Eric earned a total interest of $1,890 from both accounts.
To find the allocation between the two accounts, we set up a system of equations. The first equation represents the total amount invested:
![\[ x + (30,000 - x) = 30,000 \]](https://img.qammunity.org/2024/formulas/mathematics/college/8q4e188n62fzs6cf3p4ao1x5n6mb4g38z2.png)
Solving this equation gives \(x = 15,000\), indicating that Eric invested $15,000 in the first account and
in the second account.
The second equation represents the total interest earned:
![\[ 0.09x + 0.06(30,000 - x) = 1,890 \]](https://img.qammunity.org/2024/formulas/mathematics/college/t4t990sha48is1pc9gx4dqizqhzujm53qj.png)
Substituting
) into this equation confirms that the interest earned matches the given total. Therefore, Eric invested $15,000 in the first account, which yielded $1,350 in interest, and $15,000 in the second account, which generated $540 in interest. This balanced allocation allowed him to accumulate a total interest of $1,890 over the year.
The probable question maybe:
Question:
Last year, Eric had $30,000 to invest. He decided to invest a certain amount in an account that paid 9% simple interest per year and the remaining amount in an account that paid 6% simple interest per year. After one year, he received a total of $1,890 in interest. How much money did Eric invest in each account?
Answer:
First account:
Second account:
