Question

Solve equation by the method of your choice

Answer 1

The quadratic equation
`5x^2` - 12x = 9 is solved by setting it equal to zero and applying the quadratic formula, yielding two solutions: x = 3 and x = -0.6.

To solve the quadratic equation
`5x^2` - 12x = 9, we first need to move all terms to one side of the equation to set it equal to zero. This gives us
`5x^2` - 12x - 9 = 0. Now, we can use the quadratic formula to solve for x, which states that x = (-b ± √(
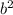`b^2` - 4ac)) / (2a), where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c = 0. In our case, a=5, b=-12, and c=-9.

Substituting these into the formula gives us x = (12 ± √(
`(-12)^2` - 4(5)(-9))) / (2(5)). We simplify this to get x = (12 ± √(144 + 180)) / 10, which simplifies further to x = (12 ± √(324)) / 10. Since the square root of 324 is 18, we have x = (12 ± 18) / 10. This yields two solutions: x = 3 and x = -0.6.

Therefore, the solutions to the equation
`5x^2` - 12x = 9 are x = 3 and x = -0.6.