Question

Among all pairs of numbers whose difference is 8​, find a pair whose product is as small as possible. What is the minimum​ product?

Answer 1

Let's denote the two numbers as x and y, where x is greater than y. The difference between the two numbers is 8, so we have the equation:

x - y = 8

Solving for x, we get x = y + 8

Now, the product of the two numbers is given by xy. Substitute the expression for x into the product:

xy = (y + 8)y

Expand the expression:

xy = y^2 + 8y

This is a quadratic expression in terms of y. To find the minimum product, we can analyze the expression and determine the value of y that minimizes it. Since the coefficient of y^2 is positive, the expression represents an upward-opening parabola, and the minimum occurs at the vertex.

The vertex form of a quadratic expression is given by y = a(x - h)^2 + k, where (h, k) is the vertex. In our case, h is given by -b/2a, where a is the coefficient of y^2 and b is the coefficient of y.

For y^2 + 8y, a = 1 and b = 8. Therefore:

h= -
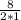`(8)/(2*1)` = -4

Now substitute h back into the equation to find k:

k = (-4)^2 + 8(-4) = 16 - 32 = -16

So, the minimum product occurs when y = -4. Now substitute y = -4 back into the equation for x:

x = (-4) + 8 = 4

The pair of numbers is x = 4 and y = -4, and the minimum product is:

xy = 4 * (-4) = -16

Therefore, the minimum product among all pairs of numbers whose difference is 8 is -16.