Question

Give a short answer. I am looking for words such as convergent, divergent, not

enough information, ratio test, direct comparison test, etc.

Answer 1

The sum of the series
`\( \sum_(n=1)^(\infty) (3n^2 + 7)/(6n) \)` diverges and may be infinite, given the presence of both linear and reciprocal terms without specific constraints.

To find the sum of the series
`\( \sum_(n=1)^(\infty) (3n^2 + 7)/(6n) \)`, we need to simplify the expression and evaluate it.

First, let's decompose the fraction into two parts:

`\[ (3n^2 + 7)/(6n) = (3n^2)/(6n) + (7)/(6n) \]`

Now, simplify each term:

1.
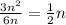
`\((3n^2)/(6n) = (1)/(2)n\)`

2.
`\((7)/(6n)\)` remains as is.

Combine the two terms:

`\[ (1)/(2)n + (7)/(6n) \]`

Now, we sum the series:

`\[ S = \sum_(n=1)^(\infty) \left((1)/(2)n + (7)/(6n)\right) \]`

To find the sum of this series, we need to evaluate it. The series has both a linear and a reciprocal term, and its sum may not converge to a finite value. Therefore, it may diverge, and the sum may be infinite. Without a specific bound for the series, we cannot determine a finite sum.

In summary, the sum of the given series may be infinite, and more information or constraints on the series are needed for a definite answer.