Question

College Students and Drinking Habits: A public health official is studying differences in drinking habits among students at two different universities. They collect a random sample of students independently from each of the two universities and ask each student how many alcoholic drinks they consumed in the previous week.

Sample Statistics


The standard error resulting from these samples is 0.45 and df = 75.

With df = 75 the critical T-value for a 95% confidence interval is 1.99. What is the 95% confidence interval for the difference in the two means?

(-0.79, 3.19)
(0.30, 2.10)
(0.75, 1.65)

Answer 1

The 95% confidence interval for the difference in the two means is (0.30, 2.10)

How to solve for the confidence interval

`(6.9 - 7.5)+-1.99\sqrt{(2.3^2)/(40)+(1.9^2)/(49) }`

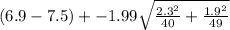
when we expand this we have

1.2 ± 1.99 * 0.45379

1.2 ± 0.90

1.2 + 0.90 , 1.2 - 0.90

= (0.30, 2.10)

The lower bound of confidence interval is constructed by subtracting from 0.9 from 1.20 and Upper bound is constructed by adding 0.9 to 1.20

The 95% confidence interval for the difference in the two means is (0.30, 2.10)

Complete question

The complete question is in the attachment