Question

Use the graph to write the formula for a polynomial function of least degree.

Need help pls asap

Answer 1

the polynomial function is

`f(x)=(1)/(6+3)(x+2)^2(x-3)=(1)/(9)(x+2)^2(x-3)`

The graph appears to show a polynomial function of the third degree with two real roots. The minimum point of the graph is at (-2,-4), which means the quadratic factor of the function must be
`(x+2)^2`. The two real roots must be to the left of -2, so we can write the polynomial as
`f(x)=a(x+2)^2(x-b)`. To determine the values of a and b, we can use the fact that the graph passes through the points (-4,4) and (4,2).

When x=-4, the function is evaluated as
`f(-4)=a(-4+2)^2(-4-b)=4a(-6-b)`. We know that f(-4)=4, so
`4a(-6-b)=4`. Solving for a, we get
`a=(1)/(6+b)`.

When x=4, the function is evaluated as
`f(4)=a(4+2)^2(4-b)=16a(6-b)`. We know that f(4)=2, so 16a(6-b)=2. Solving for a, we get
`a=(1)/(48-8b).`

Setting these two expressions for a equal to each other, we get
`(1)/(6+b) = (1)/(48-8b)`. Solving for b, we get b=3.

Therefore, the polynomial function is
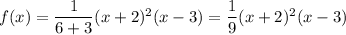`f(x)=(1)/(6+3)(x+2)^2(x-3)=(1)/(9)(x+2)^2(x-3)`.